|
||
|
|
||

|
||
|
|
||
|
The basic transmission mechanisms of the various types of optical fiber waveguide have been discussed in Chapter 2. However, the factors which affect the performance of optical fibers as a transmission medium were not dealt with in detail. These transmission characteristics are of' utmost importance when the suitabilitv of' optical fibers i'or communication purposes is investigated. Fhe transiniss'Ou characteristics of most interest are those of' attenuation (or loss) and bandwidth. The huge potential bandwidth of' optical communications helped stimulate the birth of the idea that a dielectric waveguide made of glass could be used to carry wideband telecommunication signals. This occurred, as indicated in Section 2.1 in the celebrated papers by Kao and Hockharn, and Werts, in 1966. However, at the time the idea may have seemed somewhat ludicrous as a typical block of glass could support optical transmission for at best a few tens of meires before it was attenuated to an unacceptable level. Nevertheless, careful investigation of' the attenuation showed that it was largely due to absorption in the glass, caused by impurities such as iron, copper, manganese and other transition metals which occur in the third row of the periodic table. Hence, research was stimulated towards a new aerteration of 'pure' glasses for use in optical fiber communications. A major breakthrough came in 1970 when the first fiber with an attenuation below 20 dB km-' was reported [Ref. 11 . This level of attenuation was seen as the absolute minimum that had to be achieved before an optical fiber system could in any way compete economically with existing communication systems. Since 1970 tremendous improvements have been made, leading to silica-based glass fibers with losses of less than 0.2 dB km-' in the laboratory [Ref. 21. Hence, comparatively low loss fibers have been incorporated into optical communication systems throughout the world. Moreover, as the fundamental lower limits for attenuation in silicate glass fibers have virtually been achieved, activities are increasing in relation to the investigation of other material systems which may exhibit substantially lower losses when operated at longer wavelengths. Such mid-infrared (and possibly far-infrared) transmitting fibers could eventually provide for extremely long-haul repeaterless communication assuming that, in addition to the material considerations, the optical source and detector requirements can be satisfactorily met [Ref. 2]. The other characteristic of primary importance is the bandwidth of the fiber. This is limited by the signal dispersion within the fiber, which determines the number of bits of information transmitted in a given time period. Therefore, once the attenuation was reduced to acceptable levels attention was directed towards the dispersive properties of fibers Again, this has led to substantial improvements, giving wideband fiber bandwidths of many tens of gigahertz over a number of kilometres. In order to appreciate these advances and possible future developments, the optical transmission characteristics of fibers must be considered in greater depth. Therefore, in this chapter we discuss the mechanisms within optical fibers which give rise to the major transmission characteristics mentioned previously (attenuation and dispersion), whilst also considering other, perhaps less obvious, effects when light is propagating down an optical fiber (modal noise, polarization and nonlinear phenomena). We begin the discussion of attenuation in Section 3.2 with calculation of the total losses incurred in optical fibers. The various attenuation mechanisms (material absorption, linear scattering, nonlinear scattering, fiber bends) are then considered in detail in Sections 3.3 to 3.6. The primary focus within these sections is on silica-based glass fibers. However, in Section 3.7 consideration is given to other material systems which may be employed for mid-infrared and far-infrared optical transmission. Dispersion in optical fibers is described in Section 3.8, together with the associated limitations on fiber bandwidth. Sections 3.9 and 3.10 deal with intramodal and intermodal dispersion mechanisms and included in the latter section is a discussion of the modal noise phenomenon associated with intermodal dispersion. Overall signal dispersion in both multimode and single-mode fibers is then considered in Section 3.1 1. This is followed in Section 3.12 by discussion of the modification of the dispersion characteristics within single-rnode fibers in order to obtain dispersion shifted and dispersion flattened fibers. Section 3.13 presents a brief account of polarization within single-mode fibers which includes description of the salient features of polarization maintaining fibers. Finally, nonlinear optical phenomena, which can occur at relatively high optical power levels within single-mode fibers, are dealt with in Section 3.14.
|
||
|
The attenuation or transmission loss of optical fibers has proved to be one of the most important factors in bringing about their wide acceptance in telecommunications. As channel attenuation largely determined the maximum transmission distance prior to signal restoration, optical fiber communications became especially attractive when the transmission losses of fibers were reduced below those of the competing metallic conductors (less than 5 dB km-'). Signal attenuation within optical fibers, as with metallic conductors, is usually expressed in the logarithmic unit of the decibel. The decibel, which is used for comparing two power levels, may be defined for a particular optical wavelength as the ratio of the input (transmitted) optical power Pi into a fiber to the output (received) optical power Po from the fiber as:
This logarithmic unit has the advantage that the operations of multiplication and division reduce to addition and subtraction, whilst powers and roots reduce to multiplication and division. However, addition and subtraction require a conversion to numerical values which may be obtained using the relationship:
In optical fiber communications the attenuation is usually expressed in decibels per unit length- (i.e. dB/ km) following:
where a dB is the signal attenuation per unit length in decibels and L is the fiber length
Example 3.1 When the mean optical power launched into an 8 km length of fiber is 120 m W, the mean optical power at the fiber output is 3 m W.
Determine:
Solution: (a) Using Eq. (3. 1), the overall signal attenuation in decibels through the fiber is:
= 10 log 40 = 16.0 dB (b) The signal attenuation per kilornetre for the fiber may be simply obtained by dividing the result in (a) by the fiber length which corresponds to it using Eq. (3.3) where,
hence, a dB = 16.0 / 8 = 2.0 dBkm-1
However, the link also has nine splices (at 1 km intervals) each with an attenuation of 1 dB. Therefore, the loss due to the splices is 9 dB. Hence, the overall signal attenuation for the link is:
(d) To obtain a numerical value for the input/output power raLiO, Eq. (3.2) may be used where :
A number of mechanisms are responsible for the signal attenuation within optical fibers. These mechanisms are influenced by the material composition, the preparation and purification technique, and the waveguide structure. They may be categorized within several major areas which include material absorption, material scattering (linear and nonlinear scattering), curve and microbending losses, mode coupling radiation losses and losses due to leaky modes. There are also losses at connectors and splices, as illustrated in Example 3.1. However, in this chapter we are interested solely in the characteristics of the fiber; connector and splice losses are dealt with in Section 5.2. It is instructive to consider in some detail the loss mechanisms within optical fibers in order to obtain an understanding of the problems associated with the design and fabrication of low loss waveguides.
|
||
|
3.3 Material absorption losses in silica glass fibers
Material absorption is a loss mechanism related to the material composition and the fabrication process for the fiber, which results in the dissipation of some of the transmitted optical power as heat in the waveguide. The absorption of the light may be intrinsic (caused by the interaction with one or more of the major components of the glass) or extrinsic (caused by impurities within the glass).
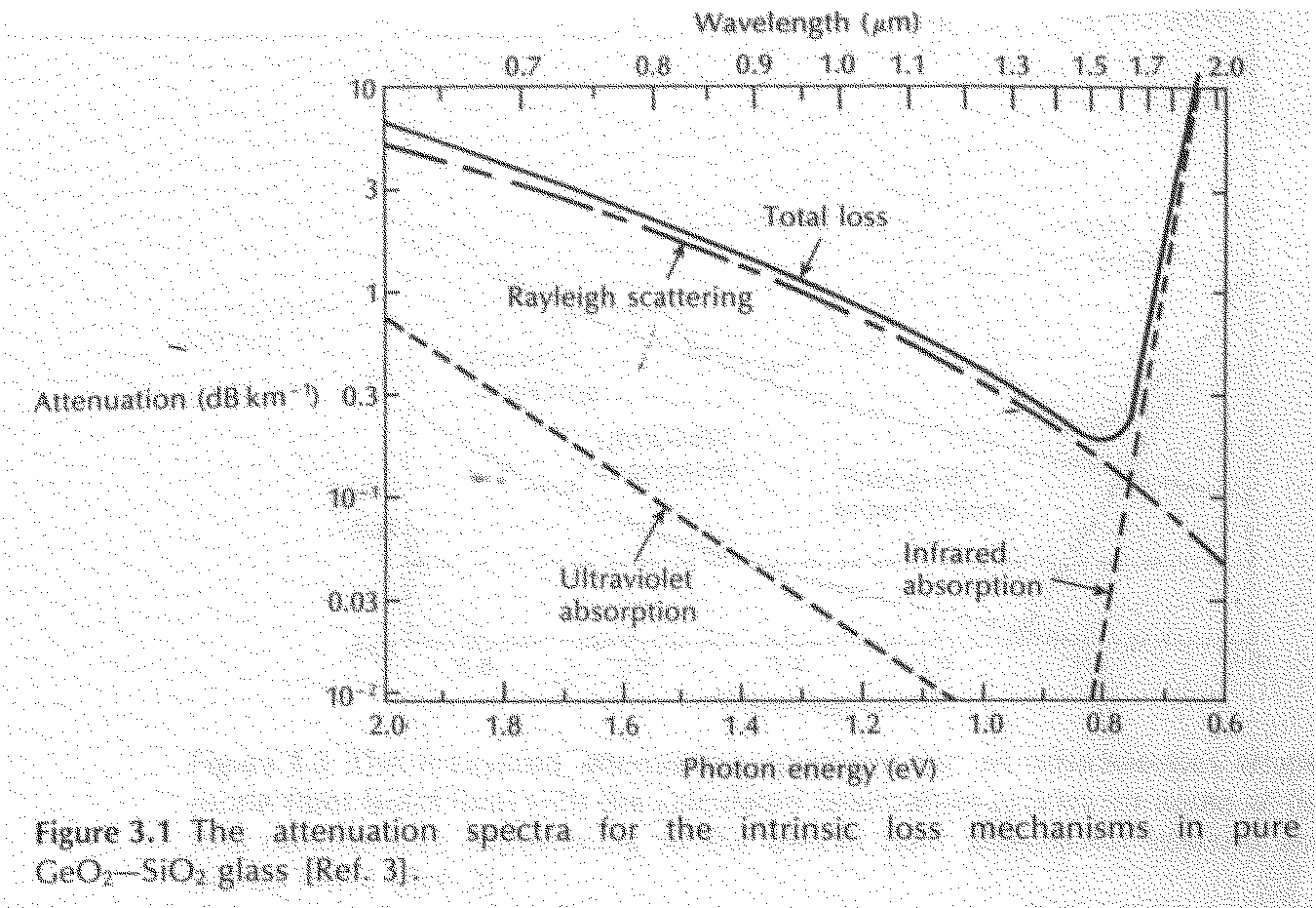
3.3.1 Intrinsic absorption An absolutely pure silicate glass has little intrinsic absorption due to its basic material structure in the near-infrared region. However, it does have two major intrinsic absorption mechanisms at optical wavelengths which leave a low intrinsic absorption window over the 0.8 to 1.7 m m wavelength range, as illustrated in Figure 3.1, which shows a possible optical attenuation against wavelength characteristic for absolutely pure glass [Ref. 3]. It may be observed that there is a fundamental absorption edge, the peaks of which are centred in the ultraviolet wavelength region. This is due to the stimulation of electron transitions within the glass bv higher energy excitations. The tail of this peak may extend into the window region at the shorter wavelengths, as illustrated in Figure 3.1. Also in the infrared and far-infrared, normally at wavelengths above 7 m m, fundamentals of absorption bands from the interaction of photons with molecular vibrations within the glass occur. These give absorption peaks which again extend into the window region. The strong absorption bands occur due to oscillations of structural units such as Si-O (9.2 m m),
P-0 (8.1 m m), B-0 (7.2 m m) and Ge-O (11.0 m m) within the glass. Hence, above 1.5 m m the tails of these largely far-infrared absorption peaks tend to cause most of the pure glass losses. However, the effects of both these processes may be minimized by suitable choice of both core and cladding compositions. For instance, in some nonoxide glasses such as fluorides and chlorides, the infrared absorption peaks occur at much longer wavelengths which are well into the far-infrared (up to 50 m m), giving less attenuation to longer wavelength transmission compared with oxide glasses.
3.3.2 Extrinsic absorption In practical optical fibers prepared by conventional melting techniques (see Section 4-3), a major source of signal attenuation is extrinsic absorption from transition metal element impurities. Sonic of the more common metallic impurities found in glasses are shown in the Table 3.1,
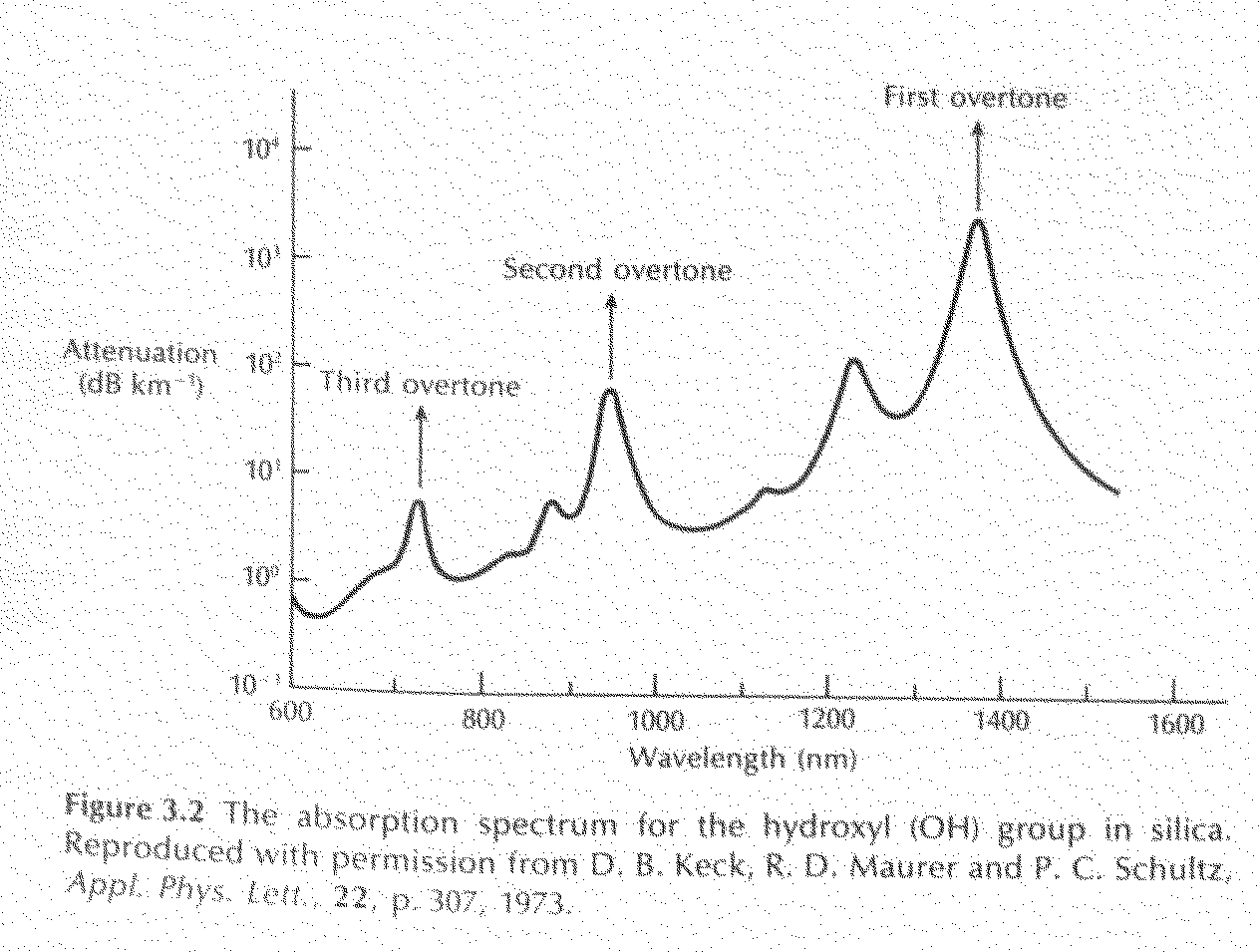
together with the absorption losses caused by one part in 109 [Ref. 4]. It may be noted that certain of these impurities, namely chromium and copper, in their worst valence state can cause attenuation in excess of 1 dB km -1 in the near-infrared region. Transition element contamination may be reduced to acceptable levels (i.e. one part in 1010) by glass refining techniques such as vapour-phase oxidation [Ref. 51 (see Section 4.4), which largely eliminates the effects of these metallic impurities. However, another major extrinsic loss mechanism is caused by absorption due to water (as the hydroxyl or OH ion) dissolved in the glass. These hydroxyl groups are bonded into the glass structure and have fundamental stretching vibrations which occur at wavelengths between 2.7 and 4.2 m m depending on group position in the glass network. The fundamental vibrations give rise to overtones appearing almost harmonically at 1.38, 0.95 and 0.72 pm, as illustrated in Figure 3.2 [Ref. 6]. This shows the absorption spectrum for the hydroxyl group in silica. Furthermore, combinations between the overtones and the fundamental SiO2 vibration occur at 1,24, 1.13 and 0.88 m m, completing the absorption spectrum shown in Figure 3.2. It may also be observed in Figure 3.2 that the only significant absorption band in the region below a wavelength of 1 m m is the second overtone at 0.95 m m which causes attenuation of about I dB km - 1 for one part per million (ppm) of hydroxyl. At longer wavelengths the first
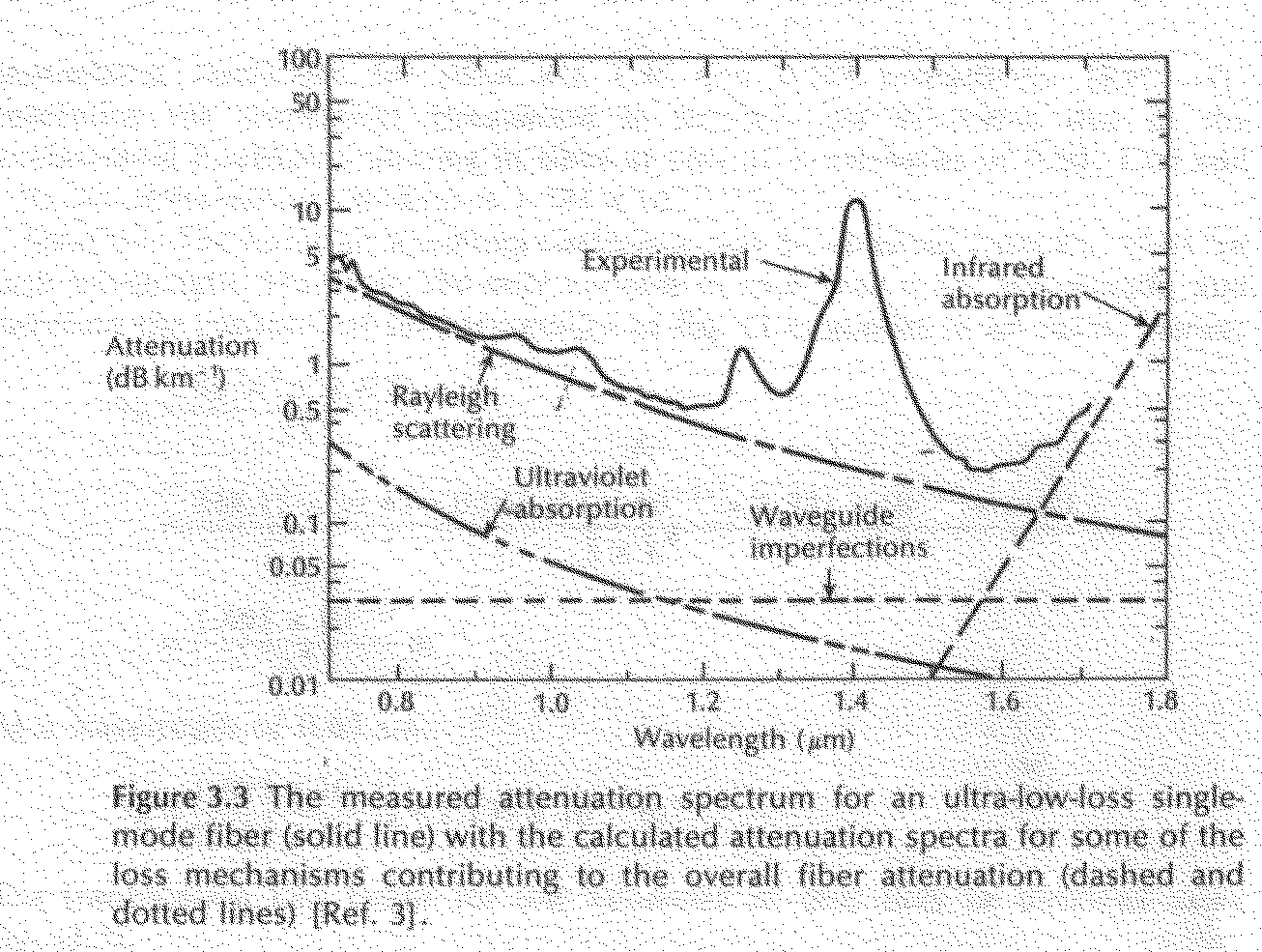
overtone at 1.38 m m and its sideband at 1.24 m m are strong absorbers giving attenuation of about 2 dB km-1 ppm and 4 dB km-1 pprn respectively. Since most resonances are sharply peaked, narrow windows exist in the longer wavelength region around 1.3 and 1.55 #m which are essentially unaffected by OH absorption once the impurity level has been reduced below one part in 10'. This situation is illustrated in Figure 3.3, which shows the attenuation spectrum of an ultra-low-loss single-mode fiber [Ref. 3]. It may be observed that the lowest attenuation for this fiber occurs at a wavelength of 1.55 m m and is 0.2 dB km-1 . This is approaching the minimum possible attenuation of around 0. 18 dB km-1 at this wavelength [Ref. 8].
|
||
|
Linear scattering mechanisms cause the transfer of some or all of the optical power contained within one propagating mode to be transferred linearlv (proportionally to the mode power) into a different mode. This process tends to result in attenuation of the transmitted light as the transfer
may be to a leaky or radiation mode which does not continue to propagate within the fiber core, but is radiated from the fiber. It must be noted that as with all linear processes there is no change of frequency on scattering. Linear scattering may be categorized into two major types: Rayleigh and Mie scattering. Both result from the nonideal physical properties of the manufactured fiber which are difficult and, in certain cases, impossible to eradicate at present.
Rayleigh scattering is the dominant intrinsic loss mechanism in the low absorption window between the ultraviolet and infrared absorption tails. It results from inhornogeneities of a random nature occurring on a small scale compared with the wavelength of the light. These inhomogeneities manifest themselves as refractive index fluctuations and arise from density and compositional variations which are frozen into the glass lattice on cooling. The compositional variations may be reduced by improved fabrication, but the index fluctuations caused by the freezingin of density inhomogeneities are fundamental and cannot be avoided. The subsequent scattering due to the density fluctuations, which is in almost all directions, produces an attenuation proportional to 1/l 4 following the Rayleigh scattering formula [Ref. 9] . For a single component glass this is given by:
where g R is the Rayleigh scattering coefficient, l is the optical wavelength, n is the refractive index of the medium, p is the average photoelastic coefficient, b c is the isothermal compressibility at a fictive temperature TF, and K is Boltzmann's constant. The fictive temperature is defined as the temperature at which the glass can reach a state of thermal equilibrium and is closely related to the anneal temperature. Furthermore, the Rayleigh scattering coefficient is related to the transmission loss factor (transmissivity) of the fiber l following the relation [Ref. 10]:
where L is the length of the fiber. It is apparent front Eq. (3.4) that the fundamental component of Rayleigh scattering is strongly reduced by operating at the longest Possible wavelength. The theoretical attenuation due to Rayleigh scattering in silica at wavelengths of 0.63, 1.00 and 1.30 Am, from Example 3.2, is 5.2, 0.8 and 0.3 dB km-1 respectively. These theoretical results are in reasonable agreement with experimental work. For instance, a low reported value for Rayleigh scattering in silica at a wavelength of 0.6328 pin is 3.9 dB km-1 [Ref. 11] . However, values of 4.8 dB km-1 [Ref. 12] and 5.4 dB km-1 [Ref. 13] have also been reported. The predicted attenuation due to Rayleigh scattering against wavelength is indicated bv a broken line on the attenuation characteristics shown in Figures 3.1 and 3.3.
Linear scattering may also occur at inhomogeneitics which are comparable in size to the guided wavelength. These result from the nonperfect cylindrical structure of the waveguide and may be caused by fiber imperfections such as irregularities in the core-cladding interface, core-cladding refractive index differences along the fiber length, diameter fluctuations, strains and bubbles. When the scattering inhomogeneity size is greater than l / 10, the scattered intensity which has an angular dependence can be very large. The scattering created by such inhomogeneities is mainly in the forward direction and is called Mie scattering. Depending upon the fiber material, design and manufacture, Mie scattering can cause significant losses. The inhomogeneities may be reduced by:
By these means it is possible to reduce Mic scattering to insignificant levels.
Optical waveguides do not always behave as completely lincar channels whose increase in output optical power is directlv proportional to the input optical power. Several nonlinear effects occur, which in the case of scattering cause disproportionate attenuation, usually at high optical power levels. This nonlinear scattering causes the optical power from one mode to be transferred in either the forward or backward direction to the same, or other modes, at a different frequency. It depends critically upon the optical power density within the fiber and hence only becomes significant above threshold power levels. The most important types of nonlinear scattering within optical fibers are stimulated Brillouin and Raman scattering, both of which are usually only observed at high optical power densities in long single-mode fibers. These scattering mechanisms in fact give optical gain but with a shift in frequency, thus contributing to attenuation for light transmission at a specific wavelength. However, it may be noted that such nonlinear phenomena can also be used to give optical amplification in the context of integrated optical techniques (see Section 10.8). In addition, these nonlinear processes are explored in further detail both following and in Section 3.14.
3.4.2.1 Stimulated Brillouin scattering Stimulated Brillouin scattering
Stimulated Brillouin scattering (SBS) may be regarded as the modulation of light through thermal molecular vibrations within the fiber. The scattered light appears as upper and lower sidebands which are separated from the incident light by the modulation frequency. The incident photon in this scattering process produces a phonon* of acoustic frequency as well as a scattered photon. This produces an optical frequency shift which varies with the scattering angle because the frequency of the sound wave varies with acoustic wavelength. The frequency shift is a maximum in the backward direction reducing to zero in the forward direction making SBS a mainly backward process. As indicated previously, Brillouin scattering is only significant above a threshold power density. Assuming that the polarization state of the transmitted light is not maintained (see Section 3.12), it may be shown [Ref 16] that the threshold power PB is given by:
where d and l are the fiber core diameter and the operating wavelength, respectively, both measured in micrometres, a dB is the fiber attenuation in decibels per kilometre and n is the source bandwidth (i.e. injection laser) in gigahertz. The expression given in Eq. (3.6) allows the determination of the threshold optical power which must be launched into a single-mode optical fiber before SBS occurs (see Example 3.3).
3.4.2.2 Stimulated Raman scattering
Stimulated Raman scattering (SRS) is similar to stimulated Brillouin scattering except that a high frequency optical phonon rather than an acoustic phonon is generated tile scattering process. Also, SRS can occur in both the forward and backward directions in all optical fiber, and may have an optical power threshold to three orders of magnitude higher than the Brillouin threshold in a particular fiber. Using the same criteria as those specified for the Brillouin scattering threshold given in Eq. (3.6), it may be shown [Ref. 16] that the threshold optical power for long single-mode fiber is given by:
PR = 5.9 X 10 -2d2l a dB watts (3.7) where d, l and a dB are as specified for Eq. (3.6).
|
||
|
Optical fibers suffer radiation losses at bends or curves on their paths. This is due tothe energy in the evanescent field at the bend exceeding the velocity of light in the cladding and hence the guidance mechanism is inhibited, which causes light energy to be radiated from the fiber. An illustration of this situation is shown in Figure 3.4. The part of the mode which is on the outside of the bend is required to travel faster than that on the inside so that a wavefront perpendicular to the direction of propagation is maintained. Hence, part of the mode in the cladding needs to travel faster than the velocity of light in that medium. As this is not possible, the energy
associated with this part of the mode is lost through radiation. The loss can generally be represented by a radiation attenuation coefficient which has the form [Ref. 19]:
a r = c 1 exp ( -c2 R )
where R is the radius of curvature of the fiber bend and c 1 and c2 are constants which are independent of R. Furthermore, large bending losses tend to occur in multimode fibers at a critical radius of curvature R, which may be estimated from [Ref. 20]:
Rc = 3n12l / 4p (n12 - n22) (3.8)
It may be observed from the expression given in Eq. (3.8) that potential macrobending losses may be reduced by:
|
||
|
3.6 Mid-infrared and far-infrared transmission
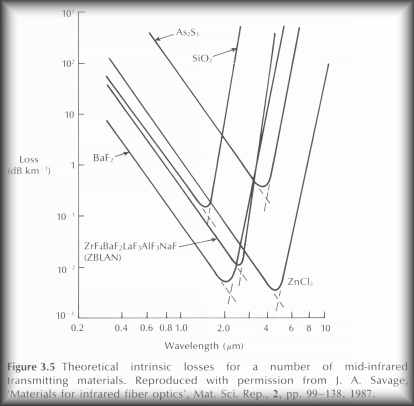
In the near-infrared region of the optical spectrum, fundamental silica fiber attenuation is dominated by Rayleigh scattering and multiphonon absorption from the infrared absorption edge (See Figure 3.2). Therefore, the total loss decreases as the operational transmission wavelength increases until a crossover point is reached around a wavelength of 1.55 um where the total fiber loss again increases because at longer wavelengths the loss is dorninated by the phonon absorption edge. Since the near fundamental attenuation limits for near-infrared silicate glass fibers have been achieved, more recently researchers have turned their attention to the mid-infrared (2 to 5 m m) and the far-infrared (8 to 12 m m) optical wavelengths. In order to obtain lower loss fibers it is necessary to produce glasses exhibiting longer infrared cutoff wavelengths. Potentially, much lower losses can be achieved if tile transmission window of the material can be extended further into the infrared bv utilizing constituent atoms of higher atomic mass and if it can be drawn into fiber exhibiting, suitable strength and chemical durability. The reason for this possible loss reduction is due to Rayleigh scattering which displays a X` dependence and hence becomes much reduced as the wavelength is increased. For example, the scattering loss is reduced by a factor of 16 when the optical Wavelength is doubled, Thus it may be possible to obtain losses of the order of 0.01 dBkm-' at a wavelength of 2.55 m m, with even lower losses at wavelengths of between 3 m m and 5 m m [Ref. 23]. Candidate glass forming systems for mid-infrared transmission are fluoride, fluoride -chloride, chalcogenide and possibly oxide. In particular, heavy metal oxide glasses based on, bismuth and gallium oxides offer a near equivalent transmittance range to many of the fluoride glasses and hence show promise if their scatter losses can be made acceptably low [Ref. 24] . Chalcogenide glasses, which generally comprise one or more of the elements S, Se and Te, together with one or more elements Ge, Si, As and Sb, are capable of optical transmission in both the mid-infrared and far-infrared regions.* However, research activities into far-infrared transmission using chalcogenide glasses, halide glasses and halide crystal fibers are at present mainly concerned with radiometry, infrared imaging and power transmission rather than telecommunications [Ref. 25]. The research activities into ultra-low-loss fibers for long-haul repeaterless communications have to date centred on the fluorozirconates, with Zirconium fluoride (ZrF4) as the major constituent and nuorides of bariurn, lanthanurn, aluminium, gadolinium, sodium, lithium and occasionally lead added as modifiers and stabilizers [Ref. 26]. Such alkali additives improve the glass stability and working characteristics. Moreover, hafniurn tetrafluoride (HfF4) can be substituted for ZrF4 to vary the refractive index and form fluorohafnate glasses. Both these glass systems offer transmittance to a wavelength of around 5.5 m rn [Ref. 23]. In order to fabricate low loss, long length fluoride fibers a basic problem concerned with reducing the extrinsic losses remains to be resolved [Ref. 27] . At present the most critical and difficult problems are associated with the minimization of the scattering losses resulting from extrinsic factors such as defects, waveguide imperfections and radiation caused by mechanical deformation. The estimated losses of around 0.01 dB km-' at a wavelength of 2.5 m m for ZrF4-based fibers are derived from an assessment of the extrinsic losses due to ultraviolet and infrared absorptions together with Rayleigh scattering. However, experimental losses obtained so far remain significantly higher (i.e. one order of magnitude) than this estimated value. Nevertheless, it is useful to consider the theoretical characteristics for intrinsic losses obtained for a irange of materials which are displayed in Figure 3.5 [Ref. 28], The effect of increasing the atomic weight of the anion from oxide to fluoride may be clearly observed. Although the theoretical losses shown in Figure 3.5 cannot yet be achieved in practical fiber, progress has been made in relation to the fabrication of heavy metal fluoride glass fibers, particularly for single-mode operation [Ref. 29].
Materials such as ZnC12 and AS2S3 are also being considered for mid-infrared transmission since this is their region of minimum loss, as can be observed in Figure 3.5. In addition these glasses offer potential for far-infrared transmission applications as fiber lengths of a few metres may prove sufficient for use with CO2, laser radiation.* Moreover, both rnonocrystalline and polycrystalline halide fibers [Ref. 23] as well as hollow core glass fibers [Ref. 30] are being studied to assess their p0tentizIl for high power transmission applications. A commercial example in the former case is Kristen 5 (KRS-5) fiber fabricated from T1Br and T1I produced by Horiba of Japan [Ref. 25] .
|
||
|
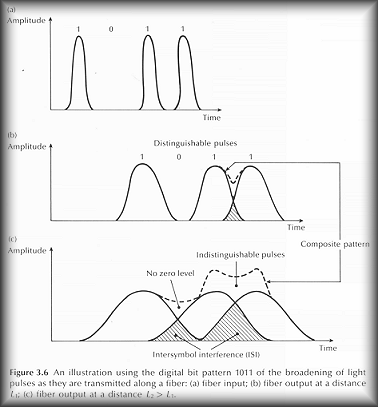
Dispersion of the transmitted optical signal causes distortion for both digital and analog transmission along optical fibers. When considering the major implementation of optical fiber transmission which involves some form of digital modulation, then dispersion mechanisms within the fiber cause broadening of the transmitted light pulses as they travel along the channel. The phenomenon is illustrated in Figure 3.6, where it may be observed that each pulse broadens and overlaps with its neighbours, eventually becoming indistinguishable at the receiver input. The effect is known as intersymbol interference (ISI). Thus an increasing number of errors may be encountered on the digital optical channel as the ISI becomes more pronounced. The error rate is also a function of the signal attenuation on the link and the subsequent signal to noise ratio (SNR) at the receiver. This factor is not pursued further here but is considered in detail in Section 11.6.3. However, signal dispersion alone limits the maximum possible bandwidth attainable with a particular optical fiber to the point where individual symbols can no longer be distinguished.
For no overlapping of light pulses down on an optical fiber link the digital bit rate BT must be less than the reciprocal of the broadened (through dispersion) pulse duration (2t ). Hence:
This assumes that the pulse broadening due to dispersion on the channel is t which dictates the input pulse duration which is also t . Hence Eq. (3.10) gives aconservative estimate of the maximum bit rate that may be obtained on an optical fiber link as 1/2t . Another more accurate estimate of the maximum bit rate for an optical channel with dispersion may be obtained by considering the light pulses at the output to have a Gaussian shape with an rms width of s . Unlike the relationship given in Eq. (3.10), this analysis allows for the existence of a certain amount of signal overlap on the channel, whilst avoiding any SNR penalty which occurs when intersynibol interference becomes pronounced. The maximum bit rate is given approximately by (see Appendix B):
It must be noted that certain sources [Refs. 31, 32] give the constant term in the numerator of Eq. (3.1 1) as 0.25. However, we take the slightly more conservative estimate given, following Olshansky [Ref. 9] and Gambling et al. [Ref. 33] . Equation (3.11) gives a reasonably good approximation for other pulse shapes which may occur on the channel resulting from the various dispersive mechanisms within the 6ber. Also, a may be assumed to represent the rnis impulse response for the channel, as discussed further in Section 3.10.1. The conversion of bit rate to bandwidth in hertz depends on the digital coding format used. For metallic conductors when a nonreturn to zero code is employed, the binary one level is field for the whole bit period t . In this case there are two bit Periods i it one wavelength (i.e. two bits per second per hertz), as illustrated in Figure 3.7(a) . Hence the maximum bandwidth B is one half the maximum data rate or
However, when a return code is considered, as shown in Figure 3.7(b), the binary one level is held for only part (usually half) the bit period. For this signalling scheme the data rate is equal to the bandwidth in hertz (i.e. one bit per second per hertz) and thus BT = B. The bandwidth B for metallic conductors is also usually defined by the electrical 3 dB points (i.e. the frequencies at which the electrical power has dropped to one half of its constant maximum value). However, when the 3 dB optical bandwidth of a fiber is considered it is significantly larger than the corresponding 3 dB electrical bandwidth for the reasons discussed in Section 7.4.3. Hence, when the limitations in the bandwidth of a fiber due to dispersion are stated (i.e. optical bandwidth Bopt), it is usually with regard to a return to zero code where the bandwidth in hertz is considered equal to the digital bit rate. Within the context of dispersion the bandwidths expressed in this chapter will follow this general criterion unless otherwise stated. However, as is made clear in Section 7.4.3, when electro-optical devices and optical fiber systems are considered it is more usual to state the electrical 3 dB bandwidth, this being the more useful measurement when interfacing an optical fiber link to electrical terminal equipment. Unfortunately, the terms of bandwidth measurement are not always made clear and the reader must be warned that this omission may lead to some confusion when specifying components and materials for optical fiber communication systems. Figure 3.8 shows the three common optical fiber structures, multimode step index, multimode graded index and single-mode step index, whilst diagrammatically illustrating the respective pulse broadening associated with each fiber type. It may be observed that the multimode step index fiber exhibits the greatest dispersion of a transmitted light puls'e and the multimode graded index fiber gives a considerably improved performance. Finally, the single-mode fiber gives the minimum pulse broadening and thus is capable of the greatest transmission bandwidths which are currently in the gigahertz range, whereas transmission via multimocle step index fiber is usually limited to bandwidths of a few tens of megahertz.
Intramodal or chromatic dispersion may occur in all types of optical fiber and results from the finite spectral linewidth of the optical source. Since optical sources do not emit just a single frequency but a band of frequencies (in the case of the injection laser corresponding to only a fraction of a per cent of the centre frequency, whereas for the LED it is likely to be a significant percentage), then there may be propagation delay differences between the different spectral components of the transmitted signal. This causes broadening of each transmitted mode and hence intramodal dispersion. The delay differences may be caused by the dispersive properties of the waveguide material (material dispersion) and also guidance effects within the fiber structure (waveguide dispersion).
Pulse broadening due to material dispersion results from the different group velocities of the various spectral components launched into the fiber from the optical source. It occurs when the phase velocity of a plane wave propagating in the dielectric medium varies nonlinearly with wavelength, and a material is said to exhibit material dispersion when the second differential of the refractive index with respect to wavelength is not zero. The pulse spread due to material dispersion may be obtained by considering the group delay t g, in the optical fiber which is the reciprocal of the group velocity n , defined by Eqs. (2.37) and (2.40). Hence the group delay is given by: t g = db / dw = 1/c ( n1-l dn1/dl ) (3.13)
where n, is the refractive index of the core material. The pulse delay t m due to material dispersion in a fiber of length L is therefore:
For a source with rms spectral width s l and a mean wavelength l , the rms pulse broadening due to material dispersion s m may be obtained from the expansion of Eq. (3.14) in a Taylor series about l .
|
||